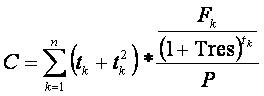In questo articolo ci occupiamo degli indicatori di rischio delle obbligazioni. Prima cercheremo di spiegarti nel modo più semplice possibile che cosa è la duration delle obbligazioni, in seguito come puoi calcolarla. Se hai bisogno di comprendere meglio le caratteristiche tecniche di un’obbligazione potrebbe esserti utile la mia guida di approfondimento. Se hai bisogno di stimare il rendimento di un’obbligazione puoi usare il nostro tool gratuito.
Indice
Che cos’è la duration delle obbligazioni
La duration è l’indicatore di rischio di tasso interesse delle obbligazioni più noto. Essa viene chiamata anche durata media finanziaria. E’ stata sviluppata da Maculay nel 1938, ma esistono anche la:
- Fisher-Weil duration;
- la Cox, Ingersoll, Ross duration.
La duration è la media aritmetica delle scadenze in cui il titolo effettua pagamenti (cedole e/o capitale). Ciascun periodo è ponderato per il rapporto tra il valore attuale delle singole prestazioni ed il prezzo tel quel del titolo. Quindi la formula è:
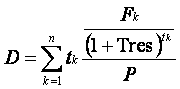
- n: Numero dei flussi di cassa
- F: k-esimo flusso di cassa
- K: Scadenza del k-esimo flusso
- P: Prezzo Tel Quel del titolo
La duration è una misura di tempo. Il calcolo della duration associa ad ogni scadenza l’importanza di ciascun flusso (attualizzato) rispetto al valore complessivo del titolo. La duration è espressa nella stessa unità temporale in cui sono misurate le scadenze dei flussi che, inoltre, coincide con il periodo al quale è riferito il TRES , tipicamente è espressa in anni. A eccezione degli zero coupon, risulta sempre inferiore alla durata residua del titolo.
Quindi caratteristiche della duration sono:
- Le obbligazioni con maggiore vita residua presentano, a parità di tutte le altre condizioni, una maggiore duration.
- I titoli obbligazionari con cedole minori presentano a parità di tutti gli altri fattori una maggiore durationdei titoli aventi cedole maggiori.
- Le obbligazioni zero coupon hanno a parità di altre condizioni, duration più elevata dei titoli con cedole di pari vita residua; infatti per i primi la duration coincide con la vita residua, per i secondi la duration è minore della vita residua.
- La duration è inversamente correlata con il Tres: se i rendimenti sono maggiori (minori), la duration è minore (maggiore).
Duration modificata
La duration, tuttavia, non è utile al solo scopo di distinguere titoli ad “alto” e “basso” rischio di tasso, ma anche per quantificare le variazioni che il prezzo di un titolo obbligazionario subisce in seguito alla variazione dei tassi di mercato. Per giungere a tale risultato è necessario procedere al calcolo della duration modificata. Quindi la formula è:
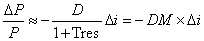
L’utilizzo della duration modificata come indicatore in grado di “cogliere” la variazione dei prezzi al variare dei tassi, presenta un limite evidente. Tale limite è identificabile nel fatto che la duration modificata si basa sull’ipotesi che la relazione prezzo-rendimento sia di tipo lineare. In realtà tale relazione presenta un andamento curvilineo. La convessità è l’indicatore che permette di correggere questo errore. L’indicatore di convessità, tuttavia, non sostituisce la duration modificata, ma si combina ad essa.